Appearance
实现一个3D饼图
当拿到UI给的上面3D饼图 (图为实际效果,可鼠标交互) 的设计图时,相信大多数小伙伴都会撂下一句:“实现不了,改设计”,我的第一反应是:“Echarts这么强大,应该有现成吧?做出来没有问题”,但是我翻遍 Echarts 官方示例和自定义示例,我发现我高估 Echarts 了,Echarts 没有现成的 3D饼图。
网上能查找到的一个近似的是实现是ECharts 3D 饼图近似实现 ,网上其他所有的实现都是基于这篇文章改编的。我心想:这种方式实现的效果虽然不怎么理想,但是我可以读懂它的代码后给他自定义美化呀,于是乎我便研究了它的源码,但是看了它的源码,我始终无法理解它是如何实现扇形的,作者duang的一下甩出下面一段" 曲面参数方程",令我百思不得其解:
点击查看源码
javascript
function getParametricEquation(startRatio, endRatio, isSelected, isHovered) {
// ......
// 返回曲面参数方程
return {
u: {
min: 0,
max: Math.PI * 2,
step: Math.PI / 100
},
v: {
min: 0,
max: Math.PI,
step: Math.PI / 50
},
x: function (u, v) {
if (midRatio - 0.5 < 0) {
if (u < startRadian || u > midRadian + Math.PI) {
tmp = u - Math.PI - midRadian < 0 ? u + Math.PI - midRadian : u - Math.PI - midRadian;
return offsetX + Math.sin(startRadian) * tmp / (Math.PI - midRadian + startRadian) * hoverRate;
}
if (u > endRadian && u < midRadian + Math.PI) {
tmp = midRadian + Math.PI - u;
return offsetX + Math.sin(endRadian) * tmp / (Math.PI - midRadian + startRadian) * hoverRate;
}
} else {
if (u < startRadian && u > midRadian - Math.PI) {
tmp = u + Math.PI - midRadian;
return offsetX + Math.sin(startRadian) * tmp / (Math.PI - midRadian + startRadian) * hoverRate;
}
if (u > endRadian || u < midRadian - Math.PI) {
tmp = midRadian - Math.PI - u < 0 ? midRadian + Math.PI - u : midRadian - Math.PI - u;
return offsetX + Math.sin(endRadian) * tmp / (Math.PI - midRadian + startRadian) * hoverRate;
}
}
return offsetX + Math.sin(v) * Math.sin(u) * hoverRate;
},
y: function (u, v) {
if (midRatio - 0.5 < 0) {
if (u < startRadian || u > midRadian + Math.PI) {
tmp = u - Math.PI - midRadian < 0 ? u + Math.PI - midRadian : u - Math.PI - midRadian;
return offsetY + Math.cos(startRadian) * tmp / (Math.PI - midRadian + startRadian) * hoverRate;
}
if (u > endRadian && u < midRadian + Math.PI) {
tmp = midRadian + Math.PI - u;
return offsetY + Math.cos(endRadian) * tmp / (Math.PI - midRadian + startRadian) * hoverRate;
}
} else {
if (u < startRadian && u > midRadian - Math.PI) {
tmp = u + Math.PI - midRadian;
return offsetY + Math.cos(startRadian) * tmp / (Math.PI - midRadian + startRadian) * hoverRate;
}
if (u > endRadian || u < midRadian - Math.PI) {
tmp = midRadian - Math.PI - u < 0 ? midRadian + Math.PI - u : midRadian - Math.PI - u;
return offsetY + Math.cos(endRadian) * tmp / (Math.PI - midRadian + startRadian) * hoverRate;
}
}
return offsetY + Math.sin(v) * Math.cos(u) * hoverRate;
},
z: function (u, v) {
return Math.cos(v) > 0 ? 0.1 : -0.1;
}
};
}作者并没有对此段代码做出任何解释,代码经过复杂的函数计算最终得出一个扇形,看到这里,我失去了对它研究的兴趣,打算放弃。等等,我是不是找错了方向?需求是实现一个3D饼状图,我为什么不用web 3D区的扛把子——Three.js来实现呢?有了正确思路,说干就干。如果你对 Three.js 还不了解,可以先阅读 ThreeJs简单入门。
准备工作
我们先回到 ThreeJs简单入门 的代码,给页面添加一个炫酷的背景,并将 renderer 的背景填充为透明:
js
//......
const renderer = new THREE.WebGLRenderer();
renderer.setSize(window.innerWidth, window.innerHeight);
renderer.setClearColor(0x000000, 0);
document.body.appendChild(renderer.domElement);为了方便编写模型,我们引入一个坐标系,并添加一个相机控件轨道控制器 OrbitControls:
js
import {OrbitControls} from 'three/addons/controls/OrbitControls.js';
import {AxesHelper,/*......*/} from 'three';
//......
const axes = new THREE.AxesHelper(100);
scene.add(axes);
const controls = new THREE.OrbitControls(camera, renderer.domElement);AxesHelper 是Three.js的坐标工具,红,绿,蓝三色射线分别代表X,Y,Z轴,参数 100 代表坐标轴长度,AxesHelper 也相当于一个实体,所以要将其添加到场景中;
OrbitControls 是 Three.js 的相机控件轨道控制器,用于控制相机的视角,它是一个 Three.js 的插件,所以是从 Three.js 的组件包中引入的。将摄像机 camera 和渲染器dom元素 renderer.domElement 传入 OrbitControls ,就可以控制相机的视角了,你可以在上图中试着做以下操作:
- 旋转:拖动鼠标左键,手机上为单指滑动
- 缩放:滚动鼠标中键,手机上为双指缩放
- 平移:拖动鼠标右键,手机上为双指滑动
OrbitControls 操纵的并不是正方体的位置与大小,而是相机的位置与方向——相当于是观察者调整不同角度距离观测一个物体。
原理解析
首先,我们先来看看饼图的实现原理:
- 第一步,使用线条描出扇形形状
- 第二步,使用线条生成一个扇形平面
- 第三步,将扇形平面挤出成一个扇体
- 第四步,将上诉过程封装成函数,根据数据计算每个扇形的起始角度,生成每个扇体
按照上面步骤,我们一步一步来实现
线条描出扇形
清除掉正方体,我们开始使用线条来绘制扇形。
ts
import {EllipseCurve} from "three";
// ......
const arcOuterLine = new EllipseCurve(0, 0, 20, 20, Math.PI / 4, Math.PI / 4 * 3, false)
const arcInnerLine = new EllipseCurve(0, 0, 10, 10, Math.PI / 4, Math.PI / 4 * 3, false)
const arcOuterPoints = arcOuterLine.getPoints(500)
const arcInnerPoints = arcInnerLine.getPoints(500)
arcInnerPoints.reverse()
const pointArr = arcOuterPoints.concat(arcInnerPoints);上述代码会生成一个扇形轮廓的点数组,如果将这些点具象化到我们的场景中,会得到如下图的一条线段:
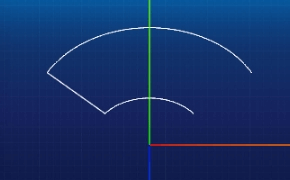
其中,线段的两段弧形是由 arcOuterLine 和 arcInnerLine构成的,他们是由 EllipseCurve 实例化而来。 EllipseCurve 可以创建一个形状为椭圆的曲线,他的参数如下:
aX椭圆的中心的X坐标,默认值为0。aY椭圆的中心的Y坐标,默认值为0。xRadiusX轴向上椭圆的半径,默认值为1。yRadiusY轴向上椭圆的半径,默认值为1。aStartAngle以弧度来表示,从正X轴算起曲线开始的角度,默认值为0。aEndAngle以弧度来表示,从正X轴算起曲线终止的角度,默认值为2 x Math.PI。aClockwise椭圆是否按照顺时针方向来绘制,默认值为false。aRotation以弧度表示,椭圆从X轴正方向逆时针的旋转角度(可选),默认值为0。
如果将 xRadius 与 yRadius 设为相等的值它将会成为一个圆。
我们使用 getPoints() 方法来获取弧形曲线上的所有点,参数 500 表示将弧形切割成 500 份,也就是生成 501 个点,这个值越大,点所连起来的线条越平滑,反之越不平滑,拖动下图中的滑动条,你会观察到不同分割份数下曲线的平滑度:
小提示
点设置越多,所绘制的图形越复杂,但越会影响性能,所以要在模型的精细程度和性能之间取舍。
ts
arcInnerPoints.reverse()
const pointArr = arcOuterPoints.concat(arcInnerPoints);这段代码的含义是将两条曲线首尾相连,因为两条曲线方向是相同的,所以我们将一条曲线的进行了翻转处理,将 pointArr 打印出来,将的到一个长度为1002的点集。
生成一个扇面
这一步比较简单,我们只需要将 pointArr 传入到 THREE.Shape 构造函数即可实例化出一个扇形,THREE.Shape 可以将点集闭合,形成一个扇形。
ts
const shape = new THREE.Shape(pointArr);如果将此图形具象化出来,会得到如下图的扇形:

挤出扇形生成扇体
这一步我们将上一步的扇形沿着 Z 轴挤出(将一个平面拉伸形成一个三维形状),形成一个扇体。
ts
const extrudeSettings = {
bevelEnabled: true,
bevelSegments: 10,
bevelThickness: 0.3,
bevelSize: 0.2,
bevelOffset: 0,
steps: 1,
depth: 10
};
const shapeGeometry = new ExtrudeGeometry(shape, extrudeSettings);
let material = new MeshPhysicalMaterial({
color: 0xff0000,
transparent: true,
opacity: 0.8,
metalness: 0.8,
roughness: 0.4
});
let mesh = new Mesh(shapeGeometry, material);
mesh.name = 'sector'
scene.add(mesh)
const light = new THREE.DirectionalLight(0xffffff, 5);
light.position.set(10, 20, 10);
scene.add(light);这样我们就得到了一个完美的扇体。
上面的代码中,我们通过 THREE.Shape 将点集转换为了一个扇形,通过 ExtrudeGeometry 将扇形沿着 Z 轴挤出,形成了一个扇体。ExtrudeGeometry 可以从一个二维图形挤出形成一个三维图形,它的参数是一个 THREE.Shape 对象, 第二个参数是一个 ExtrudeSettings 对象,它可以包含以下参数:
curveSegments曲线上点的数量,默认值是12。steps沿着挤出样条的深度细分的点的数量,默认值为1。depth挤出的形状的深度,默认值为1。bevelEnabled挤出的形状应用是否斜角,默认值为true。bevelThickness设置原始形状上斜角的厚度。默认值为0.2。bevelSize斜角与原始形状轮廓之间的延伸距离,默认值为bevelThickness-0.1。bevelOffsetDistance from the shape outline that the bevel starts. Default is 0.bevelSegments的分段层数,默认值为3。extrudePathCurve对象。一条沿着被挤出形状的三维样条线。Bevels not supported for path extrusion.UVGenerator。提供了UV生成器函数的对象。
这里我主要讲一下 ExtrudeSettings 参数中的倒角部分,它是将挤出的形状边缘的锐角变得缓和,值得注意的是,它不像生活中将一个物体棱角打磨平滑,是磨掉多余的部分,而是会改变物体的尺寸的,具体作用可以参考下图:
有了几何形状,我们为为之创建一个材质,这里用到的材质是 MeshPhysicalMaterial ,它是基于物理属性的,它可以模拟真实世界的物体外观效果,所以也有很多的属性可以设置,具体可以参考物理网格材质(MeshPhysicalMaterial) ,我们这里主要用到了 color,transparent,opacity,metalness,roughness 五个属性。
由于是物理效果材质,我们没有给它设置自发光属性,所以我们还在场景中添加了一个 DirectionalLight,DirectionalLight 是一个平行光,它可以模拟真实世界的太阳光效果。
根据数据生成3D饼图
上面我们已经了单个扇体的生成,那么我们如何将数据转换为3d饼图图表呢?
其实也很简单,只要计算出每个Item占总数据的比例,然后按照比例计算出每个扇形的起始角度即可。
我们将上面的步骤整合成一个 generateSector 函数便于调用。
点击查看源码
ts
function generateSector(outerRadius: number, innerRadius: number, startAngle: number, endAngle: number, height: number, color: ColorRepresentation) {
const arcOuterLine = new EllipseCurve(0, 0, outerRadius, outerRadius, startAngle, endAngle, false)
const arcInnerLine = new EllipseCurve(0, 0, innerRadius, innerRadius, startAngle, endAngle, false)
const arcOuterPoints = arcOuterLine.getPoints(500)
const arcInnerPoints = arcInnerLine.getPoints(500)
arcInnerPoints.reverse()
const pointArr = arcOuterPoints.concat(arcInnerPoints);
const extrudeSettings = {
bevelEnabled: true,
bevelSegments: 10,
bevelThickness: 0.3,
bevelSize: 0.2,
bevelOffset: 0,
steps: 1,
depth: height
};
const shapeGeometry = new ExtrudeGeometry(new Shape(pointArr), extrudeSettings);
let material = new MeshPhysicalMaterial({
color,
transparent: true,
opacity: 0.8,
metalness: 0.8,
roughness: 0.4
});
let mesh = new Mesh(shapeGeometry, material);
mesh.name = 'sector'
return mesh
}for循环数据列表,每一项生成一个扇体:
ts
const dataList = [
{name: '数据一', value: 100},
{name: '数据二', value: 200},
{name: '数据三', value: 300},
{name: '数据四', value: 400},
{name: '数据五', value: 500},
]
const colors = ['#f53d3d', '#ff9100', '#eeea0d', '#03c21f', '#2776de', '#00ffe1', '#ad51e8']
const maxHeight = 20
const total = dataList.reduce((total, item) => total + item.value, 0)
let startAngle = 0
const group = new Group()
const outerRadius = 20
const innerRadius = 10
for (let i = 0; i < dataList.length; i++) {
const {value} = dataList[i]
const color = colors[i]
const height = maxHeight * value / total
const angle = value / total * Math.PI * 2
const sector = generateSector(outerRadius, innerRadius, startAngle, startAngle + angle, height, color)
group.add(sector)
startAngle += angle
}
group.rotateX(-Math.PI / 2)
scene.add(group)我们循环生成了所有的扇形,然后将它们添加到了 Group 中。Group 对象是一个容器,可以包含任意数量的对象,包括 Mesh 和 Object3D,而它自身也是一个 Object3D 对象,因此我们想让它的所有子对象都进行位置,大小变换,旋转等操作只需要对 group 对象进行操作即可。这里我们将 group 对象以 x轴为中心 旋转了90度,至此我们实现了 3D 饼图:
倒角重叠优化
细心的同学会发现,在两个扇体相交的情况地方会有重叠现象,这是因为倒角会增加扇体额外体积导致扇体体积变大,从而造成重叠。解决方法有两个,一是不要倒角,将 ExtrudeGeometry 的 bevelEnabled 改为 false,二是每次计算角度时减去倒角所占的角度。如果把倒角去掉,扇形会显得十分生硬,棱角会很锋利,所以我们还是选择第二种方法:
ts
const dataList = [
{name: '数据一', value: 100},
{name: '数据二', value: 200},
{name: '数据三', value: 300},
{name: '数据四', value: 400},
{name: '数据五', value: 500},
]
const colors = ['#f53d3d', '#ff9100', '#eeea0d', '#03c21f', '#2776de', '#00ffe1', '#ad51e8']
const maxHeight = 20
const total = dataList.reduce((total, item) => total + item.value, 0)
let startAngle = 0
const group = new Group()
const outerRadius = 20
const innerRadius = 10
const bevel = 0.2
const perimeter = Math.PI * 2 * outerRadius
const bevelAngle = bevel / perimeter * Math.PI * 2
for (let i = 0; i < dataList.length; i++) {
const {value} = dataList[i]
const color = colors[i]
const height = maxHeight * value / total
const angle = value / total * Math.PI * 2
const angle = value / total * Math.PI * 2 - 2 * bevelAngle
const sector = generateSector(outerRadius, innerRadius, startAngle, startAngle + angle, height, color)
group.add(sector)
startAngle += angle
startAngle += angle + 2 * bevelAngle
}
group.rotateX(-Math.PI / 2)
scene.add(group)上面代码中,首先是计算了 bevel 占 周长 perimeter 的比例继而计算出了倒角所占的角度 bevelAngle ,在for循环中,每次循环 angle 都减去 2 * bevelAngle的角度(两边都有倒角),再重置 startAngle 时需要再加上 2 * * bevelAngle。
其实我们只做到了外圆倒角不重叠,但是再内圆还是能看到还有一点重叠的,但是是隐藏再内圆的,很难发现,所以就讲究这样了。如果你有更好的解决方法,可以与我取得联系。
添加Label
接下来我们来给图标每个Item添加上Label标签。添加标签很容易,只需要使用HTML配合CSS定位就能搞定,但是会面临一个问题,当摄像机位置发生变化后,标签的位置也会发生变化,所以我们想要的效果是在摄像机的位置变化时,更新标签的位置。Three.js提供了 CSS2DRenderer ,它可以将标签通过CSS2D方式渲染到页面上,标签会始终附着在添加标签的模型上,当摄像机发生变化时,标签的位置也会发生变化。我们可以通过 CSS2DRenderer 来实现这个效果。
关键问题有了解决方法后,我们就可以开始实现了。首先先看下面的图:
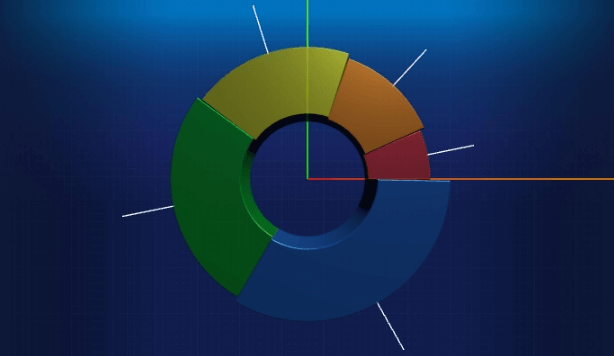
图中每个扇体旁边的白线便是我们要添加的标签的线的俯视图,要绘制这两条线,我们需要知道线段两端的两个点的坐标,起点坐标可以由扇形圆弧中心点的角度通过三角函数计算得出,终点坐标可以由相似三角形计算得出。 由此我们需要的变量:每个扇体圆弧中心点的角度和扇形半径,也就是 outerRadius。坐标的 z轴为也很好确立,为每个扇体的高度。下面我们来画出这些线段:
ts
function generateLabel(sector: Mesh, angle: number, outerRadius: number, meshHeight: number, data: {
name: string,
value: number
}, distance: number = 5, height: number = 5) {
const _distance = 1 + distance / outerRadius
const x = this.outerRadius * Math.cos(angle)
const y = this.outerRadius * Math.sin(angle)
const linePoints = []
linePoints.push(new Vector3(x, y, meshHeight))
linePoints.push(new Vector3(x * _distance, y * _distance, meshHeight + height))
const line = new Line(new BufferGeometry().setFromPoints(linePoints), new LineBasicMaterial({
color: 'white',
}))
sector.add(line)
}ts
//for循环内:
for (let i = 0; i < this.data.length; i++) {
const {value} = dataList[i]
const color = colors[i]
const height = maxHeight * value / total
const angle = value / total * Math.PI * 2
const sector = generateSector(outerRadius, innerRadius, startAngle, startAngle + angle, height, color)
group.add(sector)
generateLabel(sector, startAngle + angle / 2, outerRadius, meshHeight, this.data[i])
startAngle += angle
}我们创建了一个 generateLabel函数,它用于在扇形上添加标签。在此方法内,使用 Vector3 类来创建了线段的起点和终点,在将两个点传入 Line 类,创建出了一条线。在for循环中,通过 startAngle + angle / 2 计算出了标签的角度。
接下来,便是添加标签文字。
ts
// ......
const css2dRenderer = new CSS2DRenderer()
css2dRenderer.setSize(window.innerWidth, window.innerHeight)
css2dRenderer.domElement.style.position = 'absolute'
css2dRenderer.domElement.style.left = 0 + 'px'
css2dRenderer.domElement.style.top = 0 + 'px'
css2dRenderer.domElement.style.pointerEvents = 'none'
document.body.appendChild(css2dRenderer.domElement)
// ......
const render = () => {
css2dRenderer.value?.render(scene, camera.value!);
renderer.value?.render(scene, camera.value!);
requestAnimationFrame(render);
}
// ......
function generateLabel(sector: Mesh, angle: number, meshHeight: number, data: {
name: string,
value: number
}, distance: number = 5, height: number = 5) {
// ......
const tagEl = document.createElement('div');
tagEl.className = 'pie-chart-3d-label'
tagEl.id = 'tag'
const tagInnerEl = document.createElement('div');
tagInnerEl.className = 'pie-chart-3d-label-inner'
tagInnerEl.innerText = `${data.name} ${data.value}`
tagInnerEl.style.position = 'absolute'
tagInnerEl.style.color = 'white'
tagInnerEl.style.borderBottom = '1px solid white'
tagInnerEl.style.whiteSpace = 'nowrap'
tagInnerEl.style.height = '20px'
tagInnerEl.style.lineHeight = '20px'
tagInnerEl.style.top = '-20px'
tagEl.appendChild(tagInnerEl)
const tag = new CSS2DObject(tagEl);
tag.position.set(x * _distance, y * _distance, meshHeight + height);
sector.add(tag)
}这段代码看起来比较长,我们分成了三个部分讲解。
第一部分:我们利用 CSS2DRenderer 对象初始化了一个 css2DRenderer,用于渲染标签,和 renderer 一样,都是渲染器,只不过css2DRenderer是可以将 html 元素渲染进3D场景的渲染器,它们都需要传入 scene 和 camera ,都需要将 domElement 添加到容器中,这里,我们对css2DRenderer.domElement额外设置了一些css样式:将其的 position 设置为 absolute,left 设置为 0,top 设置为 0,这样设置使css2DRenderer.domElement和renderer.domElement 重叠在一起,再将其pointerEvents 设置为 none,这样就不会阻止鼠标事件的传播。
第二部分:在 render 方法中,将 css2DRenderer 进行渲染。
第三部分:创建generateLabel 方法,用于在扇形上添加标签。方法内先是创建了一个 HTML 标签,这里不做赘述,然后使用 CSS2DObject 实例化了一个 tag,设置了它的 position 为 x * _distance, y * _distance, meshHeight + height,也就是标签线段末端。然后将 tag 添加到 sector 上,这样这个 tag 就会被 css2DRenderer 渲染出来。
上面的图我们发现一个问题,所有的标签的朝向都是向右的,我们需要的效果是左边的标签朝左,右边的标签朝右。
我想到的解决方法是:将生成的标签 HTML 标签全部保存起来,获取容器的中心 X轴 的值,在 OrbitControls 发生改变时,循环将标签 HTML 标签列表,将标签的位置和中心X轴的值做对比,小于X轴的标签朝左,大于X轴的标签朝右。以下是代码实现:
ts
const labelList: HTMLDivElement[] = []
function generateLabel(sector: Mesh, angle: number, meshHeight: number, data: {
name: string,
value: number
}, distance: number = 5, height: number = 5) {
// ......
const tagEl = document.createElement('div');
tagEl.id = 'tag'
const tagInnerEl = document.createElement('div');
// ......
const tag = new CSS2DObject(tagEl);
tag.position.set(x * _distance, y * _distance, meshHeight + height);
sector.add(tag)
labelList.push(tagInnerEl)
}ts
const controls = new OrbitControls(camera, renderer.domElement);
controls.addEventListener('change', useThrottleFn(() => {
updateLabelOffset()
}, 300));ts
function updateLabelOffset() {
labelList.forEach((label, index) => {
const bcr = label.getBoundingClientRect()
const labelX = bcr.x
const labelWidth = bcr.width
if (labelX + labelWidth / 2 < this.centerX) {
label.style.left = `${-labelWidth}px`
} else {
label.style.left = `0px`
}
})
}最后,解决了标签位置问题,我们将坐标系去掉,便完美地实现了3D饼图。